《强化学习的数学原理》第一章:基本概念
图书:https://github.com/MathFoundationRL/Book-Mathematical-Foundation-of-Reinforcement-Learning
作者:赵世钰
配套课程资源:https://www.bilibili.com/video/BV1sd4y167NS/
基本名词
- 网格世界 (Grid World)
我们通常用一个网格图来解释和设计强化学习中的概念和算法。网格中包含起点,终点和禁区。我们的目标是让agent通过算法找到从起点到终点的最优路线。 - 状态 (State)和行为(Action)
我们用$s_n$表示一个状态,$a_n$表示路线的行为。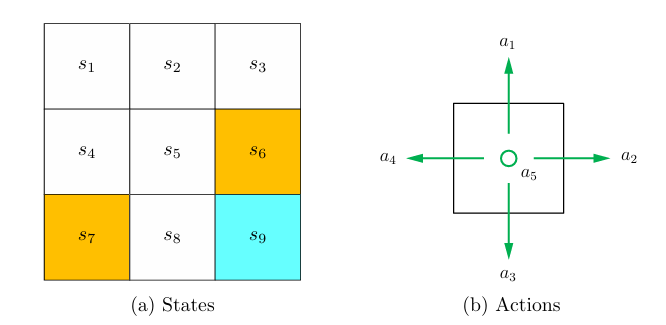
- 策略 (Policy)
策略表示agent在某个状态上采取的行动。我们用 $\pi (a_n|s_n) = p (p \in [0,1]) $ 表示采取不同策略的概率分布。 - 奖励 (Reward)
奖励指人为地设置agent在状态$s$采取行动$a$后获得的赋值,记作 $r(s,a)$。单独的 reward 并不能作为评判路线优劣的标准,因为它只是一个中间值。我们需要从一条路线的总和上来评判 reward。 - Trajectories, Returns, and Episodes
Trajectory 用来表示一个 state-action-reward 链。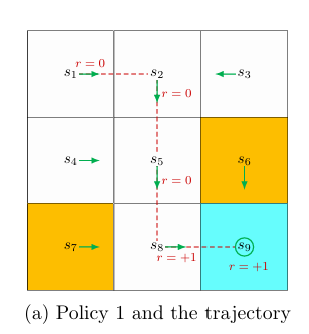
上图的 trajectory 可以表示成:
$$s_1 \overset{a_2}\rightarrow s_2 \overset{a_3}\rightarrow s_5 \overset{a_3}\rightarrow s_8 \overset{a_2}\rightarrow s_9$$
Return 表示一条 trajectory 获得的 reward 总和。在上例中
$$return = 0+0+0+1 = 1$$
这是一个 finite-length trajectory,又称为Episode。如果我们把这个定义成无限长度的 trajectory,那么$$return = 0+0+0+1+1+1+1+1+… = \infty$$
这发散了,不好。所以我们为每个 reward 加权:
$$discounted \ return = 0 + \gamma 0 + \gamma^2 0 + \gamma^3 1 + \gamma ^4 1 + \gamma^5 1 + …$$
其中$\gamma \in(0,1)$被称作 discounted rate。$\gamma$越接近0,那么后面的 reward赋权就小,得出来的策略就越短视;反之,策略就越长视。
马尔科夫决策过程 (Markov Decision Process, MDP)
- 集合 (Set)
- State: $S$ 的集合
- Action: $A(s)$ 的集合, 其中 $s \in S$
- Reward: $R(s,a)$ 的集合
- 概率分布 (Probability Distribution)
- State transition probability: 在$s$执行$a$行为,转到$s’$,记为 $p(s’|s,a)$
- Reward Probability: 记为$p(r|s,a)$
- Policy: 在$s$执行$a$的概率记为$\pi (a|s)$
- Markov Property: memoryless
$$p(s_{t + 1}|a_{t+1}, s_t, …, a_1, s_0) = p (s_{t + 1}|a_{t + 1}, s_t)$$
$$p(r_{t + 1}|a_{t+1}, s_t, …, a_1, s_0) = p (r_{t + 1}|a_{t + 1}, s_t)$$
此外,MDP 和Markov Process (MP) 的区别是,后者不涉及决策和奖励。